B+ Tree

인덱스 (Index)

인덱스란 추가적인 쓰기 작업과 저장 공간을 활용하여 데이터베이스 테이블의 검색 속도를 향상시키기 위한 자료구조이다. 데이터베이스에 따로 "어떠한 자료구조"를 갖고 독립적으로 저장되어 있으며, 실제 데이터가 아니라 실제 데이터를 찾기 위한 주소값(rid)만을 가지고 있다.

이 "어떠한 자료구조"에 가장 많이 쓰이는 것이 B+ Tree 이다. 특히, Hash Index 보다 범위 연산에 좋아 많이 쓰인다.

B-Tree

기존의 트리에서 균형을 맞춘 Balanced Tree 이다. 가끔 B minus Tree 라고 부르는 사람들이 있던데, B-Tree 에서 - 는 단지 dash 일 뿐이다.

기존의 트리는 어떤 노드는 깊이가 깊고, 어떤 노드는 얕을 수 있었다. 이 균형을 맞추기 위한 트리가 B-Tree 이다. 또한 이 구조가 인덱스를 구성하기 좋았다.

https://velog.io/@emplam27/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EA%B7%B8%EB%A6%BC%EC%9C%BC%EB%A1%9C-%EC%95%8C%EC%95%84%EB%B3%B4%EB%8A%94-B-Tree

삽입/삭제 과정은 다음을 참고하자. https://velog.io/@emplam27/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EA%B7%B8%EB%A6%BC%EC%9C%BC%EB%A1%9C-%EC%95%8C%EC%95%84%EB%B3%B4%EB%8A%94-B-Tree

[자료구조] 그림으로 알아보는 B-Tree

여기에서 더욱 활용하기 좋게 나온 것이 B+ Tree 이다.

B+ Tree

https://velog.io/@emplam27/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EA%B7%B8%EB%A6%BC%EC%9C%BC%EB%A1%9C-%EC%95%8C%EC%95%84%EB%B3%B4%EB%8A%94-B-Plus-Tree

실제 인덱스는 B+ Tree로 이루어져 있다.

B-Tree와 달리 리프노드에만 데이터 저장 가능하다. 때문에 데이터를 탐색하려면 리프 노드까지 내려와야 하지만, 높이가 보통 작아서 크게 문제되지 않는다.

또한 리프노드끼리 double-linked-list 구조로 되어있기 때문에 탐색 시 리프 노드에서 주변을 탐색할 수 있다. 이는 삽입, 삭제 시에도 굉장한 도움이 되고, 범위 탐색에 도움이 되어 인덱스에서 활용하는 가장 큰 이유가 된다.

 

이 때, 트리의 차수는 미리 정해져 있는데, 각 노드에는 적어도 차수만큼의 데이터가 들어가 있어야 한다. (루트 노드 제외) 또한 차수의 2배 이하의 데이터가 들어가 있다. 예를 들어 차수가 2이면, 각 노드에는 2개 이상 4개 이하의 데이터가 들어가있다.

차수가 2인 B+ Tree의 예시

보통 차수는 100이다. 그리고 보통 3분의 2만 채워져 있다. 즉, 200의 3분의 2인 133 정도 채워져 있다는 것이다.

그렇다면 높이가 h인 트리는 133^h 만큼의 데이터를 커버할 수 있다. h=3 이면 230만개, h=4 이면 3억개 정도이다. 즉 높이가 3인 트리가 230만개의 데이터를 처리할 수 있다. 높이는 곧 탐색의 기본적인 횟수인데, B+ Tree는 다른 자료구조에 비해 탐색이 엄청나게 빠르다는 것이다. (다만, 삽입과 삭제 연산 시 노드의 병합, 분리가 일어날 경우 너무 복잡한 일이 일어난다. 따라서 인덱스는 변경보다 조회가 많이 일어나는 컬럼에 설정하는 것이 좋다.)

만약, 데이터를 삭제해 차수보다 데이터의 개수가 작아진다면 노드끼리 합친다. 또한 데이터를 추가해 데이터가 차수의 2배보다 많아진다면 분할한다.

이 과정에 대해 자세히 알아보자.

삽입

어느 노드도 분할되지 않고 단지 삽입만 될 경우는 다루지 않겠다.

단말 노드 분리

우선, 단말 노드가 분리되는 경우이다. 노란색 형광펜 부분에 7* 라는 데이터가 들어와야 한다. 따라서 분리해야 한다.

단말 노드가 분할될 때는 copy-up을 한다. 2,3,5,7,13 중 중앙값인 5를 copy-up 해서 새로운 인덱스 엔트리를 만든다. 자연스럽게 기존의 왼쪽 노드에는 d개, 새로 생긴 오른쪽 노드에는 d+1 개가 할당된다.

인덱스 노드 분리

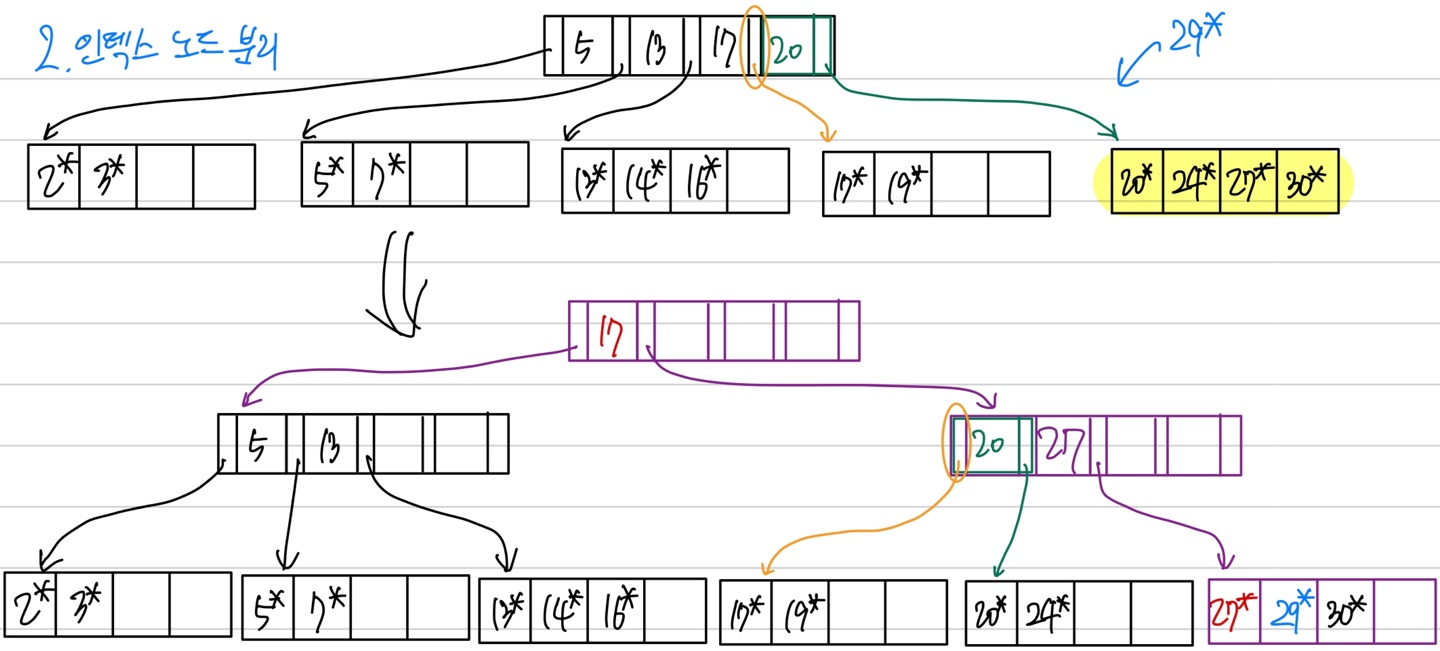
인덱스 노드까지 분리되는 경우이다. 노란색 형광펜 부분에 29* 라는 데이터가 들어와야 한다. 따라서 분리를 했는데, 분리 후 생성된 인덱스 엔트리를 넣을 인덱스 노드도 분리해야 하는 상황에 처한다.

이 경우 5,13,17,20과 copy-up 된 인덱스 엔트리 27 중에 중앙값인 17을 push-up한다. (copy-up이 아니다.) 따라서 새로운 인덱스 노드가 생긴다.

이 때, 루트 노드까지 분할이 생긴다면 (위의 경우이다.) 트리의 높이가 증가하게 된다. 이것은 굉장히 심각한 오버헤드이다.

삭제

re-distribution

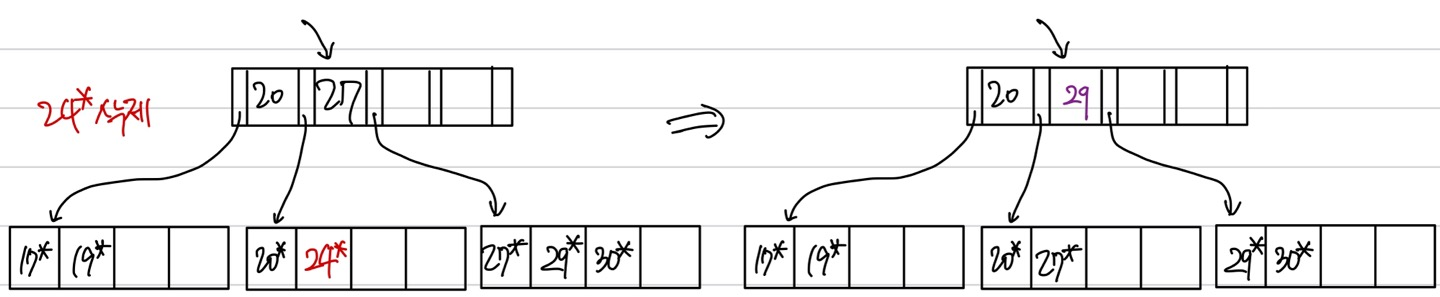
삭제 시 노드 안의 데이터가 (차수-1)개가 된다면 주변의 sibling을 탐색해 가져온다. 그림의 24* 가 삭제되어 오른쪽 노드에서 27*를 갖고 왔다. 이 때, 오른쪽 노드를 가리키는 인덱스 엔트리 값이 달라져야 한다. 이 때 값이 copy-up 된다.

merge

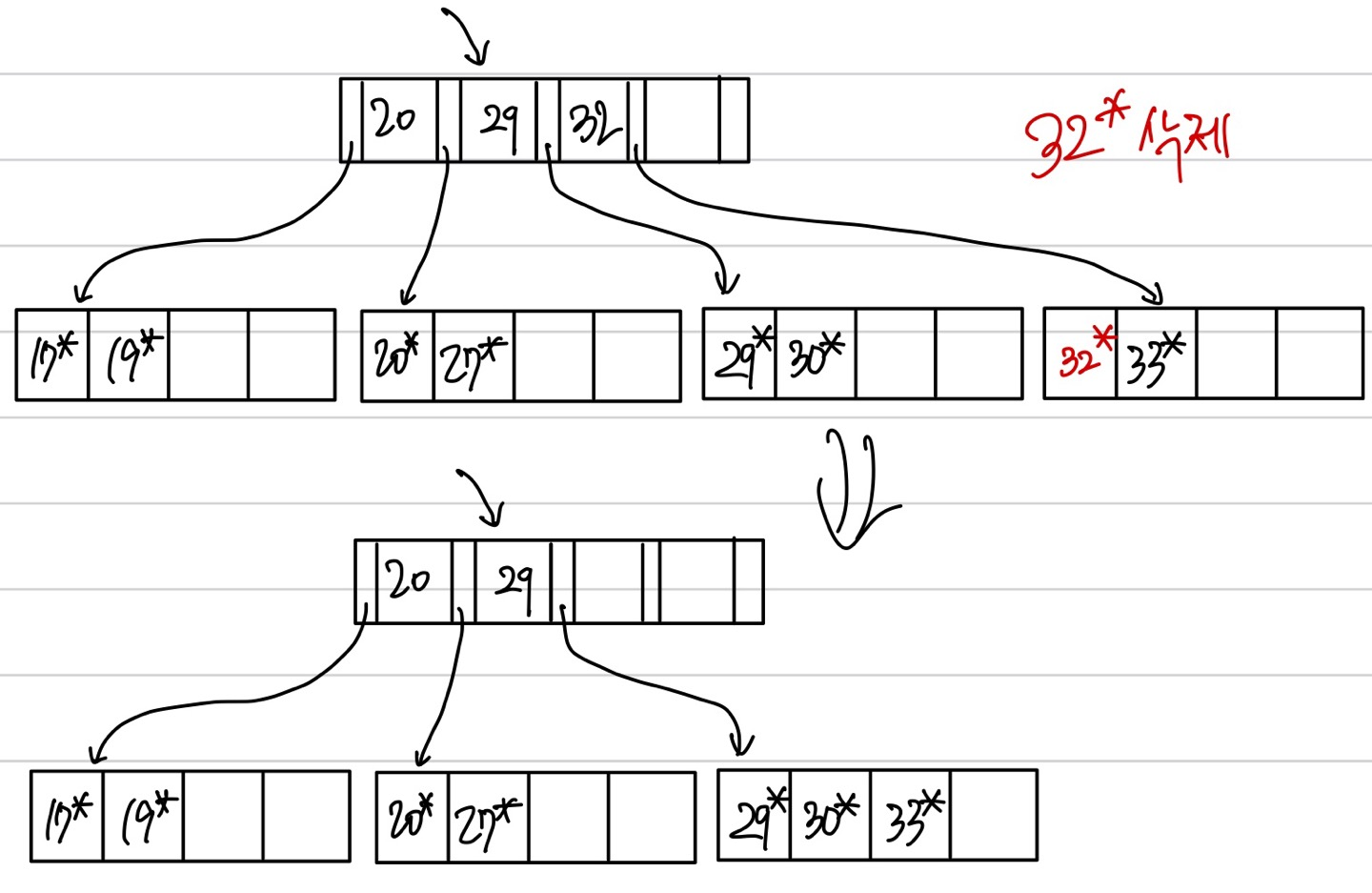
위 그림에서 32*를 삭제하려고 할 때, 어떻게 재분배를 해도 차수보다 데이터가 적어진다. 이럴 땐 sibling 노드와 merge한다. 삭제할 노드에 포함된 인덱스 엔트리를 지우면 된다. 그림에선 32 가 해당된다.

만약 인덱스 노드도 (차수-1)개가 되면 부모 노드에서 엔트리를 가지고 온다. 이를 pull-down 이라 한다.

부모 노드도 (차수-1)개가 되면 다른 자식에게서 push-up 한다.

그것도 안되면 부모가 자식과 merge한다.